Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории
Средняя скорость движения - это отношение полного пути пройденного объектом на общее время затраченное на это путешествие
Естественно предположить, что если объект часть общего пути прошел за одно время, другую часть за другое время, а третью за третье время, то средняя скорость будет являтся отношением всех частей пути на все затраченное время.
А если известно например части пути и скорость объекта на каждом пути ? Не среднее арифметическое же брать от всех скоростей... хотя очень часто именно так и поступают впервые большинство учеников, да и взрослых тоже
На самом деле, при известных частях пути и скоростей на участке формула будет следующая
наверняка догадались как она получилась из предыдущей формулы.
Если в задании пути буду обозначаться как часть от общего ( например, первая половина пути, 2/3 пути и т.п.) то, учитывая что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость будет определятся как
Пример:
Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.
Решение:
Ответ: 60 км/час
И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.
Правда есть еще четвертый вариант, но он практически никогда не встречается в задачах. Это когда встречаются комбинированные данные, например: Пешеход, преодолевает путь из точки А в точку Б. Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час. Какое расстояние между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час
Смотрим вот на эту формулу
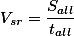
и думаем
Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)
Теперь со временем
На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути. Не пугайтесь что получилось "время равно одной десятой пути". Оно потом понадобится..
Время на втором участке известно и равно 1 час
Напишем нашу формулу по полученным данным
Выразим расстояние от точки А до точки Б через среднюю скорость и получим
Поставим значение средней скорости получим что общее расстояние которое преодолел пешеход равно 4 километра и почти 286 метров
Сложновато? Зато интересно и увлекательно.
Из последней формулы вытекает "парадоксальный" вывод: При средней скорости приближающейся к 10 км/час расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще становится отрицательным.
Что хотелось бы по этому поводу сказать. не всегда надо бездумно подвергать анализу последнюю формулу, особенно когда знаменатель обращается в ноль.
Взяв предыдущую формулу - мы бы увидели что при средней скорости в 10 км/ч , расстояние просто будет неопределено. То есть при заданных условиях средняя скорость никак не может быть больше 10 км/час.