| Полученные параметры столкновения двух объектов |
|
|
|
|
|
|
|
|
Рассмотрим задау столкновение двух тел в лобовой атаке друг на друга. Описательную часть, что это, для чего это - опустим. Нет необходимости копировать школьные учебники физики.
Но хотелось бы напомнить, что там рассматриваются два пограничных состояния:
- столкновение абсолютно упругих тел
- столкновение абсолютно неупругих тел
Но таких тел (абсолютно упругих/не упругих) в природе фактически не встречается, и нам была бы интересна универсальная (одна) формула которая объединит эти два состояние и позволит нам рассчитывать параметры объектов после столкновения при частично упругом ударе.
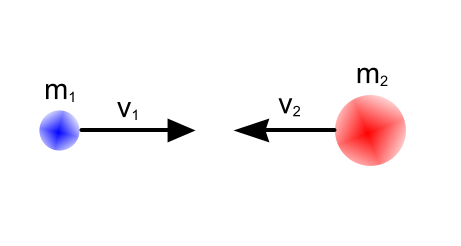
Скорость первого объекта после соударения вычисляется по формуле
m_2k}{m_1+m_2})
А скорость второго
m_1k}{m_1+m_2})
коэффициент обозначаемый k - называется коэффицент восстановления.
Может меняться от нуля до единицы.
При значении 0 - объекты абсолютно не упругие.
При значении 1 - объекты абсолютно упругие.
Что плохого в этом коэффициенте? То, что кроме как опытным путем, его не найдешь. Плюс к этому коэффициент меняется от исходных скоростей объектов.
Теперь насчет энергии теряемой при соударении. Если учитывать этот коэффицент то формула имеет вид
}(v_1-v_2)^2(1-k^2))
И опять, какой следует из этой формулы вывод?
При абсолютной упругом столкновении (k=1) потери энергии никакой нет. То есть суммы импульсов объектов до столкновения и после столкновения равны.
Бот позволяет рассчитывать недостающие параметры при столкновении двух тел. То ли известны скорости после удара и массы, тогда можете найти исходные скорости, то ли известна энергий удара и скорости объектов, тогда можно будет узнать их массы до столкновения, ну или рассчитывать параметры при других вариантах.
Удачных расчетов!