Вычисление приближенной правильной дроби

Выражение или значениеm для которого рассчитываются приближенные значения

Рассчитываем элементы непрерывной дроби для числа

Приближение дроби а также его абсолютное отклонение от точного значения

Надеюсь всем, кто читает данную статью известно различие между рациональной и иррациональной числом?

Если нет, то напомним что рациональное число всегда можно выразить точным(!) отношением двух целых чисел

Например 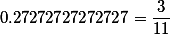$0.27272727272727=\frac{3}{11}$

Иррациональное же число никогда нельзя выразить точно через отношение двух целых чисел.

Но зато, мы иррациональное число можем представить в виде приближений двух чисел и с той точностью которая нам необходима.

Например 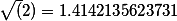$\sqrt(2)=1.4142135623731$

Нарисуем ряд дробей которые будут нам давать все более приближенные значения иррационального числа

Первое приближение понятно это

$\sqrt(2)=\frac{1}{1}=1$

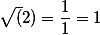
Второе приближение это

$\sqrt(2)=\frac{7}{5}=1.4$

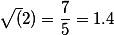
Третье приближение

$\sqrt(2)=\frac{141}{100}=1.41$

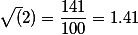
Четвертое приближение

$\sqrt(2)=\frac{707}{500}=1.414$

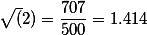
и так далее

Таким образом мы можем определять дроби которые могут представить нам с нужной точностью любое иррациональное число.

Бот этого сайта выдает список всех возможных приближений через рациональную дробь, до той точности которая возможна в языке PHP

Поиск по сайту