| Вы ввели следующие элементы массива |
![Введенное выражение]() |
| Определитель(детерминант) матрицы равен |
|
Этот калькулятор позволяет рассчитывать определитель(детерминант) квадратной матрицы любой размерности.
оределитель матрицы с комплексными коэффициентами можно найти по этой ссылке
Расчет определителя комплексной матрицы
В 1850 г. английский- математик Джеймс Джозеф Сильвестр (1814— 1897) ввел в математику понятие «матрица» для обозначения прямоугольного упорядочения чисел. Сильвестр известен тем, что давал фантастические названия математическим объектам. Матрицей должно называться место, в котором что-то развивается или возникает. Мы будем понимать матрицу в смысле упорядочения. Матрица есть математическая конструкция, представляющая собой осмысленное схематическое упорядочение других математических конструкций, находящихся построчно в линейной зависимости.
С 1853 г. к изучению матриц приступил Вильям Рован Гамильтон (1805—1865), а с 1858 г. — Артур Кэли (1821—1895). Основополагающее значение понятия матрицы для математики было осознано лишь к концу XIX в. Существенную роль в дальнейшем развитии матричного исчисления сыграл Г. Фробениус (1849—1917). Созданное алгебраистами матричное исчисление было в 1925 г. использовано Вернером Гейзенбергом для описания квантовой механики.
В 1942 г. Фельдткайлер ввел матричное исчисление в электротехнику для расчета электрических сетей. Причиной того, что матричное исчисление так поздно стало применяться вне «чистой» математики, является уровень развития вычислительной техники. При логарифмировании многократное чередование операций сложения и умножения, как это имеет место в случае линейных зависимостей (при вычислении скалярных произведений), требует значительного времени. Счетные машины, напротив, весьма удобны для проведения таких расчетов, поскольку произведения могут суммироваться в их памяти.
Лишь очень недавно матричное исчисление нашло широкое применение в экономике. Например, при планировании промышленного производства необходим большой объем часто повторяющихся вычислений (в частности, определение затрат рабочего времени и материалов для выполнения данной производственной программы). Так, перемножение объемов продукции на разнообразные нормы затрат (рабочего времени, зарплаты, материалов и др.) занимает массу времени, но может быть очень быстро осуществлено с помощью электронно-вычислительных устройств. В предположении, что имеющиеся зависимости линейны, матричное исчисление очень удобно для математического рассмотрения таких экономических и технологических задач. В математическом обеспечении ЭВМ имеются специальные подпрограммы для проведения расчетов с матрицами и их применения в экономике.
На практике, однако, часто возникают задачи, которые нелинейны. Поскольку задачи, формулирующиеся в виде систем линейных уравнений, легко обозримы и решаемы, то, естественно, необходимо исследовать вопрос о том, можно ли нелинейные задачи приближенно представить линейными зависимостями. В этом случае говорят о линеаризации соответствующей задачи. Для решения линеаризованной задачи можно применить матричное исчисление.
Синтаксис
Для тех, кто использует JABBER клиента op2 <значения матрицы>
Матрица должна быть квадратной, то есть число столбцов и строк должно быть одинаково.
Как например здесь
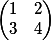
Значением матрицы являются действительные числа, а также любое математическое выражение, результатом которого будет действительное число.
Элементы матрицы вводятся по принципу слева направо и сверху вниз, в одну или несколько строк.
Каждый элемент матрицы должен быть разделен пробелами.
Нет никаких ограничений на количество элементов матрицы.
Примеры
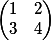
Значит в запросе надо писать op 1 2 3 4
и в ответе получим ответ -2
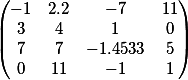
Записываем элементы
-1 2.2 -7 11 3 4 1 0 7 7 -1.4533 5 0 11 -1 1
Ответ
Матрица квадратная 4х4.
Определитель такой матрицы равен
-317.74292