Сложение комплесных чисел. Прорисовка промежуточных значений
Исходные вектора (комплексные числа)
График изменения результирующего вектора
| Результат сложения комплексных чисел |
|
| Модуль результирующего вектора |
|
| Аргумент(угол) в градусах результирующего вектора |
|
Этот калькулятор был мной создан самым первых в начале 2013 года, и является основоплагающим кирпичиком во всех последующих калькуляторах, которые вы можете видеть на сайте
Выводить его на просторы интернет было как то глупо, рассчитывая на то, что уж складывать комплексные числа могут даже дети.
Но, после того как мы смогли создавать графики, появилось обширное поле для визуального восприятия, наших действий и действий бота. Кроме этого есть небольшая информация, которая пригодится для изучающих комплексные числа.
Зачем они нам, эти комплексные числа?
Разумный вопрос. В далекие времена, когда жил и здравствовал Архимед, ни о каких числах, кроме целых и положительных ( ну и дробей с этими числами) не шло. Это и логично, как у землепашца могут быть минус 5 быков? Это нонсенс как 3/4 землекопа, Математика была чисто прикладным инструментом, для решения жизненных задач.
Но жизнь шла, сначала появились иррациональные (лат. irrationalis- неразумные) числа, которые возникают когда из целого числа извлекают например квадратный или кубический корень. В общем виде иррациональное число это такое число которое с абсолютной точностью нельзя выразить в виде дроби двух целых чисел
Потом появились трансцендентные (transcendens — переступающий, превосходящий, выходящий за пределы) числа - такие числа, которые невозможно выразить с помощью конечного количества операций над рациональными и(или) иррациональными числами.
Самое знаменитое и известное трансцендентное число это ПИ=3.1415926......
Но мы отвлеклись.
Так вот, мнимым (комплексным) числам казалось нет места, до тех пока математики не стали пытаться вычислить корни кубического уравнения. Джероламо Кардано - итальянский математик, который смог найти формулу вычисления корней кубического уравнения, в своих изысканиях столкнулся с одной "незуразностью".
Да он мог вычислять по своим формулам, всегда один вещественный корень, по любым данным, кроме одного нюанса.
Если кубическое уравнение имело три вещественных корня, например такое 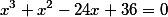 , то при промежуточных вычислениях по своим формулам, Кардано сталкивался с тем, что необходимо было извлекать квадратный корень из отрицательного числа. В то время это было табу и как обходить такую "несуразность" никто не знал.
, то при промежуточных вычислениях по своим формулам, Кардано сталкивался с тем, что необходимо было извлекать квадратный корень из отрицательного числа. В то время это было табу и как обходить такую "несуразность" никто не знал.
Уверенный в правильности своих формул, Кардано пытался найти объяснение и возможность обойти извлечения корня из отрицательного числа.
В конце концов пришлось допускать условие, что корень отрицательного числа тоже будет чему то равняться. Решили корень из минус единицы обозначать символом i (от латинского imaginarius (фиктивный)). Именно от латинского, а не от английского как иногда пишут.
Ох уж эти допущения условия...
Николай Коперник, тоже при расчетах небесных сфер, тоже допустил условие, о том что планеты вращаются вокруг Солнца. Кстати всегда интересовало почему сожгли Бруно, который жил позже чем Коперник, а вот Коперника не тронули, хотя именно он фактически внедрил гелиоцентрическую систему в практические расчеты.
Оказалось, что Коперник, во первых был очень осторожен и свою книгу "О вращении небесных сфер" предварил душевным текстом Римскому Папе, и вся книга была пронизана, верой в ГЕОцентрическую систему и учение Аристотеля о сферах.
А про ГЕЛИОцентрическую систему он говорил, что мол, смотрите такая система много упрощает, мы уходим от 48 эпициклов при расчетах положения планет, эта система упрощает расчеты календарей и прочих астрономических методик. Но, это только для вычислений, а так я верю в величие церкви и что все планеты вращаются вокруг Земли.
Может именно это помогло ему не попасть под инквизицию, а может и то, что свою книгу он отдал в печать за 1 год до смерти, и печатная версия вышла в мир, тогда когда Коперника уже не было в живых.
Так вот, комплексные числа были до тех пор "мнимыми" ( то есть они допускались при расчетах, а куда их еще девать, никто не знал), пока математики не увидели что комплексное число прекрасно уживается с (отображается) декартовой системой координат. Оказалось что вектора сил, можно представить в виде комплексного числа показательного вида, и сложение сил приложенных к какой либо точке, равно сумме этих векторов, и мы получаем не только результирующую силу, но и направление движения точки.
Вот это открытие открыло широчайшие возможности комплексных чисел. Физика, электротехника, механика - все стало использовать комплексные числа.
Наш бот, складывает комплексные числа, которые мы ввели, отображает на графике эти числа в виде векторов и выдает результат в виде промежуточных результирующих векторов.
Удачи в расчетах!
Сложение комплексных чисел |
2015-03-19 07:23:18 |
Варламов Дмитрий |
Алгебра |
Сложение комплексных чисел. Прорисовка промежуточных значений и вычисления модуля и аргумента |
сложение, комплексное, число, модуль, аргумент, график