При попытке вычислить
определитель квадратной матрицы, при выборе определенного алгоритма решения, возникает задача вычисления количество транспозиций двух множеств.
О чем же идет речь?
Пусть у нас есть строка 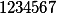 и строка
и строка 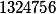 .
.
Попробуем подсчитать, сколько же нам надо сделать перестановок, что бы из второй строки получилась первая.
Перестановкой мы здесь будем обозначать действие во второй строке, при котором цифра 5(в шестой позиции слева) перемещается на 5 позицию, а цифра 7 ( в пятой позиции) перемещется на позицию номер 6.
то есть из 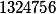 получили
получили 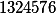 .
.
Если перестановка осуществляется только двух элементов из двух множеств, то такая перестановка называется транспозицией.
И задача состоит в том, сколько же транспозиций нам надо осуществить, что бы решить нашу задачу
Давайте на примере и решим
Первую транспозицию мы уже сделали и получили
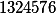
Вторая транспозиция (меняем 2 и 3 местами)
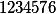
Третья (меняем 6 и 7)
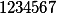
Всё, задача решена и у нас получилось 3 транспозиции.
Что же интересного в количестве транспозиций?
Во первых - их оптимальное/минимальное количество не может быть больше чем элементов в множестве минус один. Не знаю как насчет доказательств, но это объективно так.
Во вторых - если мы будем делать перестановки "не оптимально", количество может быть и больше чем три ( для нашего примера). Но главное не изменится - чётность/нечетность результата.
То есть для нашего примера количество перестановок будет всегда(!!) нечетным.
Это важнейший вывод в комплексе со свойствами определителя матрицы, нам поможет при вычислениях детерминанта матрицы определить его знак.
Расчет количества транспозиций никак не связан с классической формулой расчета расстояния Левенштейна ( минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой), по простой причине что удалять и вставлять символы мы не можем.
Бот, по заданной уникальной строке символов (цифры, английские или русские буквы) не длинее 20 символов включительно, а также ( если она задана), по опорной строке к которой необходимо привести исходную, той же длины и с теми же символами, рассчитывает количество транспозиций, и выводит в каждой строке каждое промежуточное действие.
Где еще может пригодится этот бот? Ну например для определения сколько же надо сделать перестановок в анаграмме, что бы получилось другое слово
Как пример вертикаль — кильватер
Получим что транспозиций будет 8
вот еще апельсин — спаниель
В это случае понадобится 5 транспозиций
а вот например на английском языке
nectar - trance
Для того что бы превратить слово
nectar в trance
Необходимо сначала удалить из nectar
0 символов
потом добавить в nectar
0 символов
И осуществить 3 транспозиции
Доработатав первоначальную идею, можем теперь представить и работу с аннаграммами. Но все таки ограничения есть, но мы их рассмотрим на примерах.
Пример первый. Сколько нам необходимо транспозиций, что бы из слова вертикаль придумать слово кильватер?
Этот пример удобен тем что каждая буква в слове встречается только один раз. Если мы их пронумеруем, то получим что надо превратить строку из цифр
4 7 8 6 1 0 5 2 3 --> 0 1 2 3 4 5 6 7 8
Начнем?
0 7 8 6 1 4 5 2 3
0 1 8 6 7 4 5 2 3
0 1 2 6 7 4 5 8 3
0 1 2 3 7 4 5 8 6
0 1 2 3 4 7 5 8 6
0 1 2 3 4 5 7 8 6
0 1 2 3 4 5 6 8 7
0 1 2 3 4 5 6 7 8
Итого нам надо 8 перестановок/транспозиций что бы превратить одно заданное слово в другое.
Пример второй.Сколько нам необходимо транспозиций, что бы слово внимание превратить слово вениамин?
Тут несложно заметить что есть повторяющие буквы. В частности обратим свой взор на букву н.
необходимо 0 2 3 5 4 7 6 1 --> 0 1 2 3 4 5 6 7
количество транспозиций рассчитает что необходимо 4, но если мы от цифр опять перейдем к буквам, перед этим убрав совпадающие позиции, получим Е Н И М Н ---> Н И М Н Е
Е И М Н Н
Е Н М И Н
Е Н И М Н
получилось всего три транспозиции. То есть в цифрах, количество транспозиций правильно, а как только переходим к буквам получаем совсем другой результат. Ошибка возникла из-за того что у нас есть неуникальна буква Н, ,но при расчетах, бот посчитал букву Н как уникальную и учёл два раза. Поэтому и возникнул в процессе вычисления более оптимальный путь решения. Как решать пока такие казусы я еще не знаю. Есть предположения, но они требуют размышлений. Поэтому остановимся на этом этапе.
Удачных расчетов!