| Заданная матрица |
![Исходная матрица]() |
| Матрица без указанного столбца и строки |
![Выходная матрица]() |
| Алгебраическое дополнение для указанного элемента |
![Результат дополнения алгебраического]() |
Продолжаем изучать матрицы и мы добрались до такого понятия как алгебраическое дополнение.
Что же оно представляет?
Алгебраическое дополнения элемента матрицы - есть число, которое состоит из произведения определителя(детерминанта) матрицы (без строки и столбца на которой стоит элемент матрицы) и (-1) в степени суммы номера столбца и строки.
Если это перевести в наглядный вид, то получим
Исходная матрица
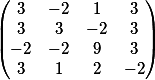
Для элемента 9, стоящего на 3 строке и 3 столбце, алгебраическое дополнение будет иметь вид
^{3+3}=-75)
Наш бот, умеет рассчитывать алгебраическое дополнение в том числе и комплексных матриц.
и вот один из примеров
|
Заданная матрица |
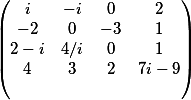 |
|
Матрица без указанного столбца и строки |
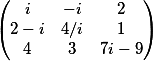 |
|
Алгебраическое дополнение для указанного элемента |
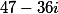 |
Удачных расчетов!