Формулы и онлайн расчет чисел Стирлинга второго рода и субфакториала.
Когда в своей работе или учебе столкнетесь с теорией вероятности или комбинаторикой, Вам пригодятся эти формулы.
Онлайн калькуляторы( на 29 сентября 2017 года)
Числа Стирлинга 1 рода
Числа Стирлинга 2 рода
Числа Белла
Число Стирлинга второго порядка
Числа Стирлинга второго рода, которые обозначают количество неупорядоченных разбиений множества из n элементов на k непустых подмножеств, вычисляются по рекуррентной формуле
=S(n,k-1)+kS(n,k))
где
=1;S(n,1)=1;S(n,n)=1)
если

то
=0)
Субфакториал
^n)
при начальном значении
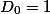
Значения субфакториала
|
n |
Dn |
|
0 |
1 |
|
1 |
0 |
|
2 |
1 |
|
3 |
2 |
|
4 |
9 |
|
5 |
44 |
|
6 |
265 |
|
7 |
1854 |
|
8 |
14833 |
|
9 |
133496 |
|
10 |
1334961 |
Число различных разбиений целого числа на целые слагаемые
Количество разбиений Pm(n) в некоторых случаях легко рассчитать самим.
Если возьмем число 5 , то разбить его можно таким образом
Одно слагаемое - 5
Два слагаемых 1+4 или 2+3
Три слагаемых 3+1+1 или 2+2+1
Четыре слагаемых 2+1+1+1
Пять слагаемых 1+1+1+1+1
Следовательно
P5(1)=P5(4)=P5(5)=1
P5(2)=P5(3)=2
В общем случае числа Pm(n) находятся как коэффициенты разложения функции
=\frac{t^n}{(1-t)(1-t^2)...(1-t^n)})
в ряд
=\sum_{m=0}^{\infty}P_m(n)t^m)