| Исходное кубическое уравнение |
![Вид уравнения]() |
| Первый корень |
![Первый корень]() |
| Второй корень |
![Второй корень]() |
| Третий корень |
![Третий корень]() |
Мы добрались до возможности решать кубические уравнения общего вида, имеющего комплексные коэффиценты.
Использовать будем методику которая называется подстановкой Виета.
Итак, когда мы из общего уравнения третьей степени 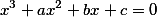
подстановкой 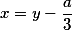
мы создали приведенное кубическое уравнение 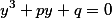
Подстановкой вида
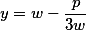
мы можем получить уравнение
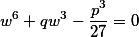
Фактически, это квадратное уравнение. Решив которое мы получим корни w.
Удивительно, но нам совершенно не важно какой корень мы возьмем от этого квадратного уравнения. Окончательный вариант все равно будет правильный.
А через них мы узнаем корни приведенного уравнения.
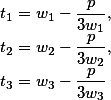
Чем удобен такой подход, от например решения уравнения по методу Кардано?
Он алгоритмически понятен и нагляден. И это главное.
Бот корректно вычисляет корни кубического комплексного уравнения, даже в том случае, если коэффициентами являются какие либо выражения ( с вещественными и/или мнимыми значениями)
Рассмотрим примеры?
x^2+xsin(3-i)-7=0)
Пишем коэффиценты слева направо (через пробел)
1 2-i sin(3-i) -7
Получаем
|
Исходное кубическое уравнение |
+x^2(2-1i)+\\+x(0.21775955+1.1634403i)+\\+(-7)=0) |
|
Первый корень |
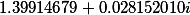 |
|
Второй корень |
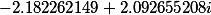 |
|
Третий корень |
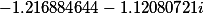 |
Вот еще один
}x^2+\\+x\frac{1}{asin(1+i)-8}+3=0)
Корни его будут равны
|
Исходное кубическое уравнение |
+\\+x^2(0.118531-0.6854142i)+\\+x(-0.133558-0.0193274i)+(3)=0) |
|
Первый корень |
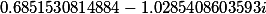 |
|
Второй корень |
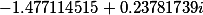 |
|
Третий корень |
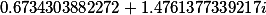 |
А вот корни обычного уравнения с вещественными числами.
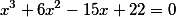
"Это легкотня" - говорит моя дочь, складывая два плюс два.
Корни такого кубического уравнения
|
Исходное кубическое уравнение |
+x^2(6)+x(-15)+(22)=0) |
|
Первый корень |
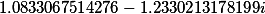 |
|
Второй корень |
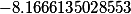 |
|
Третий корень |
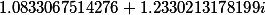 |
Удачных расчетов!