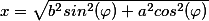Когда мы научились рассчитывать эллиптические интегралы первого и второго рода мы столкнулись с недопониманием, а где эти функции можно использовать в практическом смысле?
Что бы исправить эту ошибку начнем с темы представления некоторых интегралов, решение которых, можно представить через эллиптические функции. В открытом доступе их нет, только в бумажном виде, поэтому наверное кому то эта информация пригодится.
(b^2+x^2)}}=\frac{1}{a}F(\varphi,\frac{\sqrt{a^2-b^2}}{a}))
где 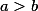 ,
, 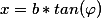
(b^2+x^2)}}=\frac{1}{a}F(\varphi,\frac{\sqrt{a^2-b^2}}{a}))
где 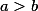 ,
, 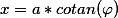
(b^2+x^2)}}=\frac{1}{\sqrt{a^2+b^2}}F(\varphi,\frac{a}{\sqrt{a^2+b^2}}))
где 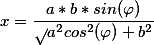
(b^2+x^2)}}=\frac{1}{\sqrt{a^2+b^2}}F(\varphi,\frac{a}{\sqrt{a^2+b^2}}))
где 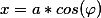
(x^2-b^2)}}=\frac{1}{\sqrt{a^2+b^2}}F(\varphi,\frac{a}{\sqrt{a^2+b^2}}))
где 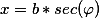
(x^2-b^2)}}=\frac{1}{\sqrt{a^2+b^2}}F(\varphi,\frac{a}{\sqrt{a^2+b^2}}))
где 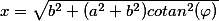
(b^2-x^2)}}=\frac{1}{b}F(\varphi,\frac{a}{b}))
где 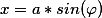
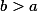
(b^2-x^2)}}=\frac{1}{b}F(\varphi,\frac{a}{b}))
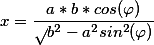
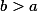
(x^2-b^2)}}=\frac{1}{a}F(\varphi,\frac{\sqrt{a^2-b^2}}{a}))
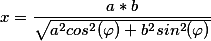
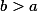
(x^2-b^2)}}=\frac{1}{a}F(\varphi,\frac{\sqrt{a^2-b^2}}{a}))
где