| Полученный полином вида f(y) |
![Введенное выражение]() |
Рассмотрим еще одну задачу связанную с полиномами. Таких типов задач Вы не встретите в задачниках, потому что она по своей сути ничему не учит. Но это совершенно не значит что решение такой задачи не используется на практике.
Почему же она не учит, спросите Вы..
Дело в том, что задача подстановки одного многочлена в другой многочлен, связан с большим числом рутинных и однообразных операций.. Запутаться там, легче легкого... а какого то смысла , ну кроме внимательности, данная задача не приносит.
Давайте все таки расскажем на примере что бот делает.
Итак, пусть у нас есть многочлен вида
=4x^4-x^3+160x^2-10)
подставим в этот многочлен заместо переменной другой многочлен
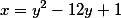
и попробуем произвести вычисления.
Выполнять вручную , как уже сказано это сложно ( в первом же действии надо квадратичный полином возводить в четвертую степень), а онлайн калькуляторов, посвященных решению данной задачи, в рунете попросту нет.
Вот эту рутину и берет на себя наш бот. Он работает также в поле комплексных чисел, что удобно для анализа.
Теперь, когда мы научились легко решать подобные задачи, можем сказать где они пригодятся.
Если считать заменяющим многочленом , одночлен такого вида 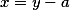
то подобным решением мы можем узнавать приведенное кубическое уравнение
И несмотря на то, что в том материале используется более простой алгоритм, сама процедура замены многочлена, воплощенная здесь, мне кажется актуальной.
В основном для исследователей, для тех, кто любит математику и видит в ней особенную красоту и гаромнию.
https://abakbot.ru/online-16
Примеры:
Выше указанный пример
=4x^4-x^3+160x^2-10)
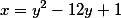
имеет решение
 = (4)*y^{8}+(-192)*y^{7}+(3471)*y^{6}+(-28188)*y^{5}+(89605)*y^{4}+(-30264)*y^{3}+(26398)*y^{2}+(-4008)*y+(154))
Пример из материала Приведенный комплексный полином 4 степени и выше
*x^{5}+(0+i)*x^{3}+(-3)*x^{2}+(0-i)*x^{1}+(2))
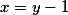
получим ответ
 = y^{6}+(0)*y^{5}+(-15)*y^{4}+(40+1i)*y^{3}+(-48-3i)*y^{2}+(30+2i)*y+(-6))
что совпадает с результатом из вышеуказанного материала
Удачных расчетов!!!