Числа Фибоначчи 3, 5, 8, 13 фигурируют в любопытном геометрическом софизме, утверждающем, что «64 = 65» или "потерянная площадь", с помощью разрезания квадрата 8X8 и складывания из него прямоугольника 5X13.
Числа Фибоначчи возникают и при описании выигрышной стратегии в древней китайской игре «дзяныпицзы», в которой двое играющих берут по очереди камни из двух кучек: либо произвольное количество из одной кучки, либо поровну из двух (выигрывает игрок, берущий последний камень).
Обнаружено, что дроби вида а/в, соответствующие винтообразному расположению листьев на стебельке растения, часто являются отношениями последовательных чисел Фибоначчи.
Для бука и орешника это отношение равно 2/3, для дуба и абрикоса — 3/5, для тополя и груши — 5/8, для ивы и миндаля —8/13, и т. д.
Числа Фиббоначи оказались неразывно связаны с так называемым "золотым сечением" , которым пользовались и практически возводили в своеобразный "культ" еще древние греки.
Золотое сечение это деление произвольного отрезка в таком отношении, что большая часть относится к меньшей, также как весь отрезок относится к большей.
Фигуры, картины, здания и все что нас окружает, по мнению древних, все должно подчинятся "золотому сечению". Правильность этого соотношения говорит о внешней гармонии наблюдаемого объекта.
Если мы хотим решить задачу и определить в числах чему же равно золотое сечение, нам необходимо решить пропорцию
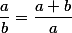
Если мы меньшую часть b примем за единицу, а a обозначим х то получим
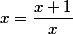
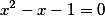
Решение этого уравнения дает нам следующий результат
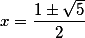
Положительное число равное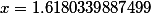 
и есть золотое сечение
Самое удивительное в том, что несмотря на явную иррациональность полученного числа именно "золотое сечение" поможет нам находить произвольное число ряда Фиббоначи. Для этого воспользуемся так называемой формулой Бине:
^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n}{\sqrt{5}})
Эта формула и используется ботом что бы Вам дать точный ответ.
И еще о "золотом сечении". Попробуем перевести число 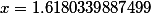в цепную или по другому, непрерывную дробь. Для этого воспользуемся ботом Непрерывные, цепные дроби онлайн
Мы увидим что иррациональное число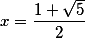 
имеет прекрасную, по своей красоте, непрерывную дробь.
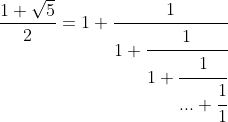
Сумма ряда Фиббоначи
Если мы внимательно посмотрим на ряд Фиббоначи 1, 1, 2, 3, 5, 8,13, 21,34 то заметим еще одну особенность.
Сумма ряда Фиббоначи равна числу этого ряда увеличенную на две позиции минус два.
Например чему равна сумма первых шести чисел этого ряда 1+2+3+5+8+13?
Она равна восьмому (шесть+два) числу Фиббоначи минус 2. то есть 34-2=32
Таким образом для того что бы посчитать сумму ряда, нет необходимости использовать циклы или суммировать каждый элемент, достаточно по формуле Бине найти число Фиббоначи, чей номер большее от заданного значения на два и вычесть два.
Синтаксис
