| Результат умножения двух матриц |
![Результат умножения]() |
Умножение матриц
Умножение матриц находит широкое применение в экономике, например при исследовании технологических связей. Процесс производства готовых изделий состоит обычно из многих ступеней.
Так, в очень простом случае из деталей собираются узлы, а уже из них и других деталей — готовые изделия. По имеющейся технологии для сборки узла необходимо определенное количество деталей.
Между количеством узлов и количеством необходимых для их производства деталей существуют линейные соотношения, т. е. задано некоторое линейное отображение множества деталей в множество узлов.
Эти соотношения могут быть заданы в виде таблиц, для которых естественной является матричная форма записи. Когда из узлов собираются готовые изделия, опять-таки имеет место линейное отображение (множества узлов в множество изделий), которое также может быть представлено1в табличной или матричной форме.
Если же нужно определить, какое количество деталей должно’быть произведено, то эти две таблицы следует заменить одной, содержащей последовательность линейных отображений связи между количеством деталей и количеством готовых изделий.
Этой замене соответствует умножение двух матриц, задающих пропорции между деталями и узлами, а также между узлами и готовыми изделиями. При этом матричное представление обеспечивает значительно большую наглядность и обозримость.
Давайте расмотрим пример
Для того чтобы рассчитать себестоимость производства изделия, необходимо определить затраты рабочего времени в часах на каждом рабочем месте для каждого изделия и каждого заказа;
Сначала рассмотрим одно рабочее место и один заказ.
Рабочий тратит рабочее время в часах, затрачиваемое на рабочем месте 1 для изготовления одного изделия разных видов.
|
Изделие тип |
A |
B |
C |
D |
|
Время |
1 |
3 |
5 |
2 |
Заказчик дал следующий заказ на предлагаемые изделия
|
Изделие тип |
A |
B |
C |
D |
|
Штук |
22 |
1 |
7 |
13 |
Для того чтобы определить затраты рабочего времени на рабочем месте 1 для выполнения данного заказа, нужно вычислить произведения 22*1 для изделия А, 3*1 для издели B и так далее, а затем сложить их. Это соответствует скалярному умножению в векторном исчислении.
То есть мы должны перемножить две матрицы
и
Получим что общие затраты рабочего на изготовление заказа составит 86 часов
Применение матриц не ограничивается только экономикой.
С помощью умножения матриц очень легко преобразовывать геометрические фигуры: переносить относительно координат, вращать, раздвигать и переворачивать.
Синтаксис
Для тех, кто использует IM клиенты: u_m матрица1;матрица2; размерность первой матрицы по горизонтали
Матрица1 и 2 являются строками содержащие элементы матрицы читая их слева направо и сверху вниз, разделенные хотя бы одним пробелом.
Примеры
Пример:1
Умножить матрицу
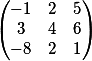
на матрицу
Делаем запрос
u_m -1 2 5 3 4 6 -8 2 1; -2 2 5 7 -1 4;3
Получаем следующее
Результат перемножения двух матриц
7 32 8 58 25 2
Размерность матрицы по горизонали равна 2
Видим что размерность равна двум значит визуально результат перемножения выглядит так
Теперь давайте перемножим те же матрицы но с другой последовательностью
u_m -2 2 5 7 -1 4;-1 2 5 3 4 6 -8 2 1; 3
Хоть элементы матрицы такие же но выглядят они по другому, так как размерность первой матрицы равна 3
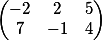
и
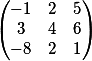
И конечно же результат перемножения будет совершенно иным
Результат перемножения двух матриц
-32 14 7 -42 18 33
Размерность матрицы по горизонали равна 3
То есть результат выглядит так