| Вы ввели корни полинома следующие |
![Введенное выражение]() |
| Полученный многочлен с заданными корнями имеет вид |
![Введенное выражение]() |
|
Описание
Часто в жизни возникает ситуация, обратной задаче нахождения корней многочлена вида
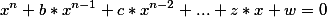
где b,c....z,w - являются коэфициентами полинома.
При n=2 получается квадратное уравнение
при n=3 кубическое и т.д.
Данный сервис позволяет решать задачу нахождения таких коэффициентов, если известны корни этого полинома.
Вроде бы простая задача, но при создании полинома четвертой степени вычислить элементы полинома уже достаточно сложно.
Смотрите сами.
Берем квадратное уравнение
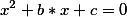
Пусть нам будут известны его корни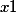 
и 
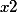
Тогда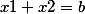 
, 
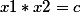
Высчитывается просто и более того основываясь на этих двух правилах, можно вычислять устно ( в уме) целочисленные корни при целых элементах квадратного уравнения.
Надо лишь, разложить 
на два множителя таким образом, что бы их сумма была равна 
Эти множители и будут корнями квадратного уравнения.
Теперь рассмотрим уравнение кубическое
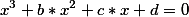
Пусть нам будут известны его корн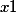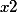и , и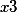 
Тогда
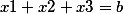
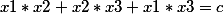
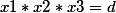
Уже сложнее. Если мы возьмем полином 4 степени и выше мы увидим что сложность вычисления элементов полинома возрастает в геометрической прогресии.
Еще сложней придется если известные корни содержат в себе комплексные числа.
Именно для упрощения подобных вычислений и был придуман этот бот.
В примерах Вы увидите как легко и просто бот создает полином произвольной степени по известным корням.
Если же Вам необходимо решить полином то ознакомтесь с статьей Расчет квадратного, кубического и 4 степени уравнения онлайн
Примеры
Определить коэффициенты многочлена когда известны следующие корни
1 2+i 2-i
|
Вы ввели корни полинома следующие |
 |
|
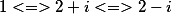Полученный многочлен с заданными корнями имеет вид |
=x^3+(-5)*x^2+(9)*x^1+(-5)) |
Где это может пригодится? Для создания задач учителями, для того что бы ученики не брали информацию из различных решебников, а пытались думать самостоятельно.
А также для создания полинома произвольной степени, если известны его корни.
