Площадь треугольника онлайн расчет

Данная страница посвящена достаточно распространенному информационному ресурсу - описанию и расчету площади произвольного треугольника. Отличие от других ресурсов, это расчет площади онлайн, непосредственно в процессе прочтения статьи

Площадь через высоту и основание

Высота треугольника
Основание куда "падает" высота треугольника

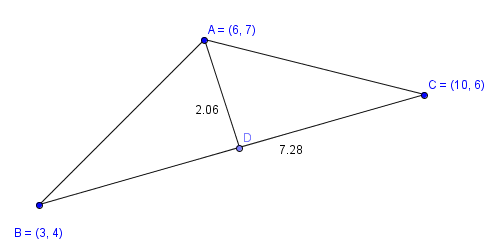
Это самая простая для запоминания формула. Словами эта формула звучит так - площадь треугольника равна половине произведения основания треугольника на его высоту.

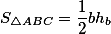
$S_{\triangle ABC}= \frac {1}{2} bh_b$

В случае прямоугольного треугольника это выражение приобретает еще более простой смысл: Площадь прямоугольного треугольника равна половине произведения двух катетов

площадь через стороны треугольника

Сторона а треугольника
Сторона b треугольника
Сторона а треугольника

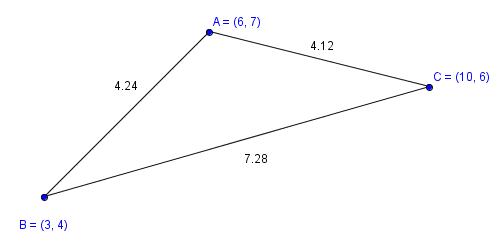
Формула Герона

$S_{\triangle ABC}= \sqrt{p(p-a)(p-b)(p-c)} = {1 \over 4}\sqrt{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}$

Площадь треугольника выраженная через стороны известна очень давно - она фигурирует в книгах, датированных 1 веком до нашей эры.

Эту формулу можно выразить по разному, благо формул расчета параметров треугольника достаточно.

Но если попытаться мыслить категориями времен до нашей эры, когда не было формул в современном преставлении, не было переменных и знаков корня, то единственной аксимомой, на базе которого, Герон, создал свою формулу, была теорема Пифагора. А так как в те времена, еще не знали иррациональных чисел, да к отрицательным у ученых было достаточно скептическое видение, то для размышлений использовались целые числа.

Самого доказательства здесь не будет, предположив только что Герон, дополнял произвольный пифагоровый треугольник до прямоугольника высчитывал его площадь, и делил на два.

Площадь через координаты вершин

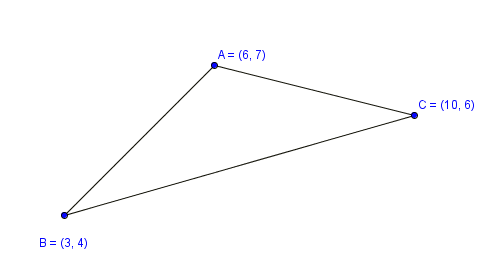
Когда известны координаты вершин треугольника, формула площади может быть выражена вот такой формулой

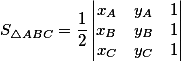
$S_{\triangle ABC}= \frac{1}{2}\begin{vmatrix} x_A & y_A & 1 \\ x_B & y_B & 1 \\ x_C & y_C & 1 \end{vmatrix}$

Определитель третьего порядка легко раскладывается, и поэтому расчет площади даже в ручном режиме не вызовет никаких затруднений.

Площадь через две стороны и угол между ними

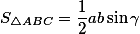
$S_{\triangle ABC}=\frac {1}{2} ab \sin \gamma$

Площадь через сторону и два угла

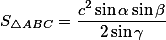
$S_{\triangle ABC}=\frac {c^2\sin\alpha\sin\beta}{2\sin\gamma}$

Редко встречающаяся задача, но и для таких исходных данных высчитали формулу. Внимательный читатаель сразу видит "ошибку". Заголовок гласит, что площадь узнается через сторону и два угла, то есть через три переменных, а в формуле присутствут все четыре. Как же так?

На самом деле ошибки никакой нет, зная одну из основных аксиом треугольника, гласящая, что сумма внутренних углов треугольника всегда(!!) равна 180 градусов

Поэтому нет ничего сложного, зная два угла треугольника, узнать третий.

Площадь через медианы треугольника

Медиана на сторону а
Медиана на сторону b
Медиана на сторону с

Красивая формула не правда ли?

$S_{\triangle ABC}=\frac{1}{\sqrt{(\frac{1}{h_{a}}+\frac{1}{h_{b}}+\frac{1}{h_{c}})(\frac{1}{h_{c}}+\frac{1}{h_{b}}-\frac{1}{h_{a}})(\frac{1}{h_{a}}+\frac{1}{h_c{1}{h_{b}})(\frac{1}{h_{a}{c}}-\fra}+\frac{1}{h_{b}}-\frac{1}{h_{c}})}}$

Как её выводили неизвестно, то что что она по своему элеганта, это не подвергается сомнению.

Поиск по сайту