| Заданная формула кривой второго порядка |
![Кривая второго порядка]() |
| Уравнение касательной в указанной точке |
![Введенное выражение]() |
Касательная к кривой
После того, как мы можем рассчитывать по произвольным координатам ту или иную кривую второго порядка на плоскости по точкам, возникла возможность рассчитать касательную в данной точке этой прямой.
Что же такое касательная? Касательная - это такая прямая которая перескает линию вида
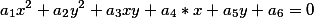
в двух совпадающих точках ( либо целиком входит в состав этой линии)
Выше приведенная формула - есть уравнение кривой второго порядка, а значит при различных заданных коэффициентах, мы можем с помощью этого бота рассчитать уравнение касательной для:
- окружности
- эллипса
- гиперболы
- прямой линии
- параболы
В дальнейшем мы рассмотрим примеры, и Вы сами сможете проверить правильность вычислений.
Уравнение касательной в общем виде выглядит так:
x+(\frac{a_3x_0}{2}+\frac{a_5}{2}+a_2y_0)y+(\frac{a_4x_0+a_5y_0}{2}+a_6)=0)
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в произвольной точке.
Синтаксис
kp2p коэффиценты;координата точки
Где коэффициенты кривой , разделенные как минимум одним пробелом, а координата точки это точка на кривой к которой и надо провести касательную.
Примеры
Вычислить уравнение касательной в точке (3:1) к окружности выраженной формулой
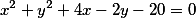
Запишем коэффиценты этой кривой, взглянув на общую формулу
и введем эти данные
kp2p 1 1 0 4 -2 -20;3 1
|
Заданная формула кривой второго порядка |
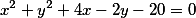 |
|
Уравнение касательной в указанной точке |
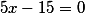 |
Получили что касательная к окружности в точности совпадает с осью абсцисс.
Провести касательную в точке (2;7) к параболе, заданной формулой
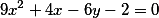
Вводим данные и получаем
|
Заданная формула кривой второго порядка |
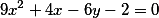 |
|
Уравнение касательной в указанной точке |
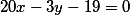 |
Как Вы видите, бот прекрасно и легко рассчитывает уравнения касательной к любой кривой второго порядка.
Удачи в расчетах!