| Уравнение первой плоскости |
![Вид уравнения]() |
| Уравнение второй плоскости |
![Вид уравнения]() |
| Уравнение прямой как пересечение двух плоскостей |
![Каноническое уравнение прямой]() |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
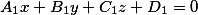
а другая плоскость уравнением вида
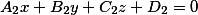
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
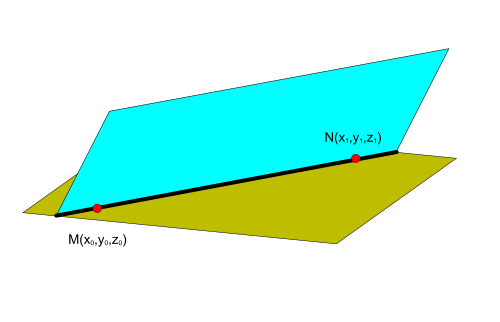
Прямая в пространстве, проходящая через две точки ) и
и ) может быть представлена в виде канонического уравнения
может быть представлена в виде канонического уравнения
\(\cfrac{x-x_0}{x_1-x_0}=\cfrac{y-y_0}{y_1-y_0}=\cfrac{z-z_0}{z_1-z_0}\)
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
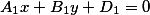
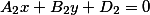
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку )
Теперь пусть z=1 и решаем систему
=0)
=0)
и получаем вторую точку )
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
\(\cfrac{x-x_0}{x_1-x_0}=\cfrac{y-y_0}{y_1-y_0}=\cfrac{z}{1}\)
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве ) и направляющий вектор
и направляющий вектор )
то уравнение прямой имеет вид
\(\cfrac{x-x_0}{m}=\cfrac{y-y_0}{n}=\cfrac{z-z_0}{p}\)
Узнав координаты точки ) ( например по выше приведенному решению) нам осталось узнать направляющий вектор.
( например по выше приведенному решению) нам осталось узнать направляющий вектор.
Для этого вычислим векторное произведение
\(\begin{pmatrix}i&j&k\\A_1&B_1&C_1\\A_2&B_2&C_2\end{pmatrix}=im+jn+kp\)
и подставив вычисленные значения в уравнение
\(\cfrac{x-x_0}{m}=\cfrac{y-y_0}{n}=\cfrac{z-z_0}{p}\)
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
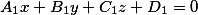
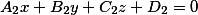
лишь тогда параллельны, когда верным становится соотношение
\(\cfrac{A_1}{A_2}=\cfrac{B_1}{B_2}=\cfrac{C_1}{C_2}\)