В этом материале, мы рассмотрим формулы, а также сможем рассчитать значения гармоник периодического прямоугольного импульса.
В высших учебных заведениях, связанных с электротехникой, нередко приходится решать подобные задачи.
Решение в общем виде заключается в разложении такого сигнала в ряд Фурье.
Наша же задача в этой статье, это непосредственный расчет гармоник такого импульса.
Какие же наши входные данные?
Это величина импульса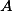 
его длительность 
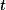и периодичность.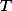
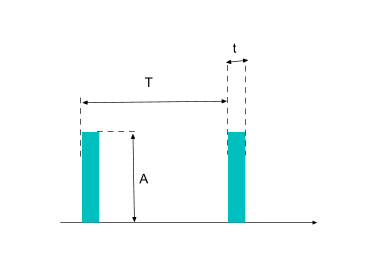
Если использовать такое понятие как скважность - отношении длительности импульса к его периоду,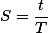 
то вполне достаточно и двух входных данных.
Расчет гармоник рассчитывается по следующим формулам
Постоянная составляющая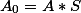 
Значение первой гармоники
)
Значение второй гармоники
)
Значение n-ой гармоники
)
Например при скважности импульса 0.5 ( и уровнем сигнала равному единице) значения первых 8 гармоник будут следующими
|
Гармоники |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0.5 |
0.637 |
0 |
-0.213 |
0 |
0.127 |
0 |
-0.09 |
0 |
Онлайн калькулятора не будет, так как формула одна и она простая. Нет необходимости под этот материал строить отдельный калькулятор.
Удачи!
